Es una característica de la sustancia sólida. Conocer su valor nos permitirá calcular la deformación que sufría un cuerpo al someterse a un esfuerzo.
Cuando en la expresión matemática del modelo del acitisida se sustituyen las ecuaciones del esfuerzo y de la deformación, se obtiene el modelo de Young,
Donde: y = f/a / al/l * y = fl/al
MODULO DE YOUNG Y LIMITE DE ELASTICIDAD P/ANGULO MATERIALES
MATERIAL MODULO DE YOUNG (Y) N/M2 LIMITE ELASTICO (LE) N/M2
Aluminio en lamina 7*10 1.4*10
Acero templado 20*10 5*10
Latón 9*10 3.8*10
Cobre 12.5*10 1.6*10
Hierro 8.9*10 1.7*10
Oro 8*10
Le = es el esfuerzo máximo que un cuerpo resiste sin perder sus propiedades elásticas.
Le = fm/a
Le = limite elástico Fm = fuerza máxima A = área de la sección transversal
sábado, 7 de junio de 2008
MODULO DE ESLATICIDAD
Es el cociente entre el esfuerzo (fuerza) aplicado a un cuerpo y la deformación producida en dicho cuerpo. También recibe el nombre de: constante del resorte o coeficiente rigidez del cuerpo sólido del que se trate.
K = Modulo de elasticidad esfuerzo / deformación
Esfuerzo (N) Deformación
0.98 0.05
1.96 0.10
2.94 0.15
3.92 0.20
4.90 0.25
K = Modulo de elasticidad esfuerzo / deformación
Esfuerzo (N) Deformación
0.98 0.05
1.96 0.10
2.94 0.15
3.92 0.20
4.90 0.25
Ejemplo de aplicacion de diferentes pesos en un resorte.
Grafica:
LEY DE HOOKE
Robert Hooke (1635 – 1703) Fisico ingles
Mientras no se exceda el límite de la elasticidad de un cuerpo la deformación elástica que sufre es directamente proporcional al esfuerzo recibido.
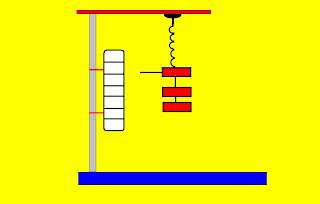
Con un resorte y una regla se comprueba la ley de Hooke al poner una pesa de 20g el resorte se estira 1cm. Pero si la pesa se cambia por una de 40g el resorte se estirara 2cm y así sucesivamente.
Mientras no se exceda el límite de la elasticidad de un cuerpo la deformación elástica que sufre es directamente proporcional al esfuerzo recibido.
Con un resorte y una regla se comprueba la ley de Hooke al poner una pesa de 20g el resorte se estira 1cm. Pero si la pesa se cambia por una de 40g el resorte se estirara 2cm y así sucesivamente.
FÍSICO ITALIANO EVANGELISTA TORRICELLI
Las velocidades la que sale un líquido por el orificio de un recipiente, es igual a la que adquiriera un cuerpo que se dejara casi libremente desde el nivel libre del líquido, hasta el nivel del orificio.
V12/2 + gh1 + p1/p1 = v22/2 +gh2 + p2/p2
V12/2 + gh1 + p1/p1 = v22/2 +gh2 + p2/p2
La velocidad con la que sale un líquido por un orificio es mayor conforme aumenta la profundidad.
PRINCIPIO DE BERNOULLI
Físico suiso Daniel Bernoulli (1700 – 1782) “La presión de un liquido que fluye por una tubería es baja si su velocidad es alta, y por el contrario; su presión es alta si su velocidad es baja”
Cuyo flujo es estacionario, la suma de las energías cinéticas, potencial y presión que tiene en un punto es igual a la suma de estas energías en cualquier otro punto.
El teorema de Daniel Bernoulli su base en la ley es de la conservación de la energía por ello en los puntos 1 y 2 la presión de la energía cinética y la energía potencial son iguales.
Cuyo flujo es estacionario, la suma de las energías cinéticas, potencial y presión que tiene en un punto es igual a la suma de estas energías en cualquier otro punto.
El teorema de Daniel Bernoulli su base en la ley es de la conservación de la energía por ello en los puntos 1 y 2 la presión de la energía cinética y la energía potencial son iguales.
PRINSIPIO DE ARQUIMEDES LA FLOTACION DE LOS CUERPOS
Cuando un cuerpo se sumerge en un liquido se observa que este ejerce una presión vertical ascendente sobre el cuerpo. Lo anterior se comprueba al introducir un trozo de madera en agua la madera es empoujada asía arriba una fuerza asía abajo si se desea mantenerla sumergida.
El empuje que reciben los cuerpos al ser introducidos en un liquido, fue estudiado por el griego Arquímedes (287- 212 ac.) quien además se destaco por sus investigaciones realizadas sobre el uso de las palancas, la geometría plana y del espacio.
Todo cuerpo sumergido en un fluido recibe un empuje ascendente igual al peso del fluido desalojado en un cuerpo totalmente sumergido en liquido todos los untos de la superficie reciben una presión hidrostáticas que es mayor conforme aumenta la profundidad, las presiones ejercidas sobre las caras opuestas se neutralizan mutuamente sin embargo esta sujeto a otras dos fuerzas opuestas, su peso que lo empuja asía abajo y el empuje de liquido que lo impulsa hacia arriba de acuerdo con la magnitud de estas dos fuerzas. Tendremos los siguientes casos:
1.- Si el peso de un cuerpo es menor al empuje que recibe, flota porque desaloja menor cantidad de liquido, si el peso del cuerpo es de menor cantidad del liquido que su volumen.
2.- Si el peso del cuerpo es igual al empuje que recibe, permanecerá en equilibrio, es decir sumergido dentro del líquido.
3.- Si el peso del cuerpo es mayor que el empuje se hunden. En este caso, como en el numero 2, al estar completamente sumergido el cuerpo desalojara un volumen de liquido igual al de su volumen.
El empuje que reciben los cuerpos al ser introducidos en un liquido, fue estudiado por el griego Arquímedes (287- 212 ac.) quien además se destaco por sus investigaciones realizadas sobre el uso de las palancas, la geometría plana y del espacio.
Todo cuerpo sumergido en un fluido recibe un empuje ascendente igual al peso del fluido desalojado en un cuerpo totalmente sumergido en liquido todos los untos de la superficie reciben una presión hidrostáticas que es mayor conforme aumenta la profundidad, las presiones ejercidas sobre las caras opuestas se neutralizan mutuamente sin embargo esta sujeto a otras dos fuerzas opuestas, su peso que lo empuja asía abajo y el empuje de liquido que lo impulsa hacia arriba de acuerdo con la magnitud de estas dos fuerzas. Tendremos los siguientes casos:
1.- Si el peso de un cuerpo es menor al empuje que recibe, flota porque desaloja menor cantidad de liquido, si el peso del cuerpo es de menor cantidad del liquido que su volumen.
2.- Si el peso del cuerpo es igual al empuje que recibe, permanecerá en equilibrio, es decir sumergido dentro del líquido.
3.- Si el peso del cuerpo es mayor que el empuje se hunden. En este caso, como en el numero 2, al estar completamente sumergido el cuerpo desalojara un volumen de liquido igual al de su volumen.
Principio de pascal
Sabemos que un liquido produce una presión hidrostática debido a su peso pero si el liquido se encierra herméticamente puede aplicársele otra presión utilizando un embolo; dicha presión se trasmitirá íntegramente a todos los puntos del liquido esto se explica si recordamos que los líquidos a diferencia de los gases y los sólidos son incomprensibles esta observación fícela el príncipe francés blaise pascal (1623 – 1662 ) quien anuncio el siguiente principio que lleva su nombre ( el principio de pascal ) toda presión que se ejerce sobre un liquido en serrado sobre un recipiente se trasmite con la misma densidad a todos los puntos del liquido y las paredes del recipiente que lo contiene. 
VAROMETRO DE MERCURIO
Es un instrumento que sirve para determinar experimental mente la presión atmosférica.
Evangelista TORRIC ELLI fue el primero en idear un barómetro. Para ello lleno con mercurio un tuvo de vidrio de casi un metro de longitud lo serró por un extremo y tapo con su dedo el extremo abierto. Invirtió en tuvo y lo introdujo en una superficie de mercurio contenido en una cubeta al retirar su dedo observo que el liquido descendía asta alcanzar el equilibrio a una altura especifica. El mercurio se izo denso de la columna de mercurio que el tubo es la que vigente la presión atmosférica.
La precion hidrostatica es aquella que origina todo liquido sobre las paredes y el fondo del resiiente que la contiene.
Donde: Ph = Peh
Ph = presión hidrostática en NM2
Pe = peso especifico del liquido en NM3
H = altura de la superficie libre al punto de nivel en metros
O bien Ph = pgh
P = densidad del liquido en Kg lm3
G = gravedad = 9.8 m/s2
Evangelista TORRIC ELLI fue el primero en idear un barómetro. Para ello lleno con mercurio un tuvo de vidrio de casi un metro de longitud lo serró por un extremo y tapo con su dedo el extremo abierto. Invirtió en tuvo y lo introdujo en una superficie de mercurio contenido en una cubeta al retirar su dedo observo que el liquido descendía asta alcanzar el equilibrio a una altura especifica. El mercurio se izo denso de la columna de mercurio que el tubo es la que vigente la presión atmosférica.
La precion hidrostatica es aquella que origina todo liquido sobre las paredes y el fondo del resiiente que la contiene.
Donde: Ph = Peh
Ph = presión hidrostática en NM2
Pe = peso especifico del liquido en NM3
H = altura de la superficie libre al punto de nivel en metros
O bien Ph = pgh
P = densidad del liquido en Kg lm3
G = gravedad = 9.8 m/s2
PRESION
La presión indica la relación entre una fuerza y el área con la cual actúa en cualquier caso en que exista presión. Una fuerza actuara en forma perpendicular sobre una superficie. Matemáticamente la presión se expresa de la siguiente forma.
P = presión ( n / m2) o pázcales
La f es la presión de la fuerza y se mide en newton.
A = área o superficie sobre la cual.
P = f / a
Cuanto mallo sea la fuerza aplicada mayor será la presión para una misma área. Cuando se aplica una misma fuerza pero el área aumenta la presión disminuye de manera inversamente proporcional al incrementote dicha área.
El resumen la presión directamente proporciona a la fuerza recibiendo inmensamente proporciona al área sobre la cual actúa.
P = presión ( n / m2) o pázcales
La f es la presión de la fuerza y se mide en newton.
A = área o superficie sobre la cual.
P = f / a
Cuanto mallo sea la fuerza aplicada mayor será la presión para una misma área. Cuando se aplica una misma fuerza pero el área aumenta la presión disminuye de manera inversamente proporcional al incrementote dicha área.
El resumen la presión directamente proporciona a la fuerza recibiendo inmensamente proporciona al área sobre la cual actúa.
DENSIDAD Y PESO ESPESIFICO
La densidad de una sustancia p = rho es una propiedad característica la masa contenida en la unidad de volumen su valor se de termina dividiendo la masa de la sustancia entre el volumen que ocupe.
El peso específico de una sustancia también es una propiedad característica y su valor se determina dividiendo su peso entre el volumen que ocupa.
P = masa / volumen densidad (kg / m3)
Pe = p / v peso especifico (n / m3)
Si recordamos que.
P = mg
Como; pe = p/ v sustituyendo pe = mg / v
La densidad igual a peso especifico dividiendo entre el valor de la aceleración gravedad.
La densidad de los líquidos se mide usando densímetros. Estos dispositivos según el nivel que alcance el líquido cuando el densímetro flota.
El peso específico de una sustancia también es una propiedad característica y su valor se determina dividiendo su peso entre el volumen que ocupa.
P = masa / volumen densidad (kg / m3)
Pe = p / v peso especifico (n / m3)
Si recordamos que.
P = mg
Como; pe = p/ v sustituyendo pe = mg / v
La densidad igual a peso especifico dividiendo entre el valor de la aceleración gravedad.
La densidad de los líquidos se mide usando densímetros. Estos dispositivos según el nivel que alcance el líquido cuando el densímetro flota.
CAPILARIDAD
La capilaridad se presenta cuando hiciste contacto entre un liquido y una pared sólida especial mente si son tubos muy delgados, (casi del diámetro de un cabello llamados capilares).
Al introducir un tubo de diámetro muy pequeño en un recipiente con agua se observara el liquido haciendo por el tuvo alcanzando una altura mayor que la superficie libre de líquidos la superficie del liquido contenido en el tuvo no es plana. Si no que forma un menisco cóncavo.
Al introducir un tubo de diámetro muy pequeño en un recipiente con agua se observara el liquido haciendo por el tuvo alcanzando una altura mayor que la superficie libre de líquidos la superficie del liquido contenido en el tuvo no es plana. Si no que forma un menisco cóncavo.
IDHERENCIA
Es la fuerza de atracción que se manifiesta entre dos moléculas de dos sustancias diferentes. Común mente la sustancia digerida se adhieren a los cuerpos sólidos.
Al sacar una barrilla de vidrio de un recipiente con agua, esta se moja porque el agua se adhiere al vidrio. Pero si la varilla de vidrio se introduce en un recipiente con mercurio, al sacarlo se observa completa mente seca lo cual indica que agua y el de herencia entre el mercurio y en el vidrio.
Al sacar una barrilla de vidrio de un recipiente con agua, esta se moja porque el agua se adhiere al vidrio. Pero si la varilla de vidrio se introduce en un recipiente con mercurio, al sacarlo se observa completa mente seca lo cual indica que agua y el de herencia entre el mercurio y en el vidrio.
COESION
Es la fuerza que mantiene unidas las moléculas de una misma sustancia si dos gotas de agua se juntan y forman una sola: lo mismo sucede con dos gotas de mercurio.
TENCION SUPERFICIAL
La tensión superficial hace que se comporte como una finísima membrana. Este fenómeno se presenta debido ala atracción entre las moléculas del líquido. Cuando se coloca el líquido en un recipiente las moléculas se atraen en todas direcciones por fuerzas iguales que se contrarrestan unas con otras que se conectan con la superficie solo son atraídas por las superiores y las laterales más cercanas.
VISCOCIDAD
Esta propiedad se origina por el rozamiento solo resta sobre otras or tal motivo, la viscosidad se puede definir como una medida de resistencia que opone un liquido al fluir si en un recipiente perforado en el centro se ase fluir por separado. Miel, leche, agua, y alcohol observaremos que cada liquido fluye con rapidez distinta, mientras mas viscoso es un liquido mas tiempo tardara en fluir.
VELOCIDAD VISCOCIDAD DE ALGUNAS SUSTANCIAS
SUSTANCIAS VISCOCIDAD POISE
POISEVILLE
AGUA A 20C 0.001 0.01
ACEITE DE 0.0970 0.97
OLIVA A 20C
MERCURIO A 20C 0.0016 0.016
GLISERINA A 20C 1.5 15
VELOCIDAD VISCOCIDAD DE ALGUNAS SUSTANCIAS
SUSTANCIAS VISCOCIDAD POISE
POISEVILLE
AGUA A 20C 0.001 0.01
ACEITE DE 0.0970 0.97
OLIVA A 20C
MERCURIO A 20C 0.0016 0.016
GLISERINA A 20C 1.5 15
HIDROSTATICA
La hidrostática es la parte de la física que estudia la mecatrónica de los fluidos y se divide en dos partes la HIDROSTATICA encargado de lo relacionado con los líquidos en reposo y la HIDRODINAMICA que estudia el comportamiento de los líquidos en movimiento.
La hidrostatica de Arquímedes se fundamenta en leyes y principios como las leyes de pascal el termino fluido se aplica a gases porque en termino ambos tienen; sin embargo un liquido es prácticamente incomprensible.
La hidrostatica de Arquímedes se fundamenta en leyes y principios como las leyes de pascal el termino fluido se aplica a gases porque en termino ambos tienen; sin embargo un liquido es prácticamente incomprensible.
ACELERASION CENTRIPETA
En el movimiento circular uniforme, la velocidad cambia constante mente su dirección.
Tal cambio se debe ala aceleración centrípeta y a que su sentido es hacia el centro y activa perpendicularmente a la velocidad tangencial.
.ac = vt2 / r ECUACION 40
.ac = w2r ECUACION 41
Un auto recorre una trayectoria circular de 304.8m una velocidad de vt193.6 k/h
¿calcular su aceleración angular?
.r = 304.8m
.vt = 193.6k/h
ac = vt2/r ac = (536m/s2) / 304.8m = 9.426 m/s2
(193.6 km / 1h ) * (1h / 3600s ) * (100m / 1km )
Un volante aumenta su velocidad de rotacion de 6 a 12 rev x s ¿Cuál es su aceleración angular?
Wi = 6 rev / s 0.6280 (12) = 7.5360
Wi = 12 rev 0.6180 (6) = 3.7680
T = 2s
A = ? a = 7.5360 – 3.7680 / 2 = 18.84 r / s2
Tal cambio se debe ala aceleración centrípeta y a que su sentido es hacia el centro y activa perpendicularmente a la velocidad tangencial.
.ac = vt2 / r ECUACION 40
.ac = w2r ECUACION 41
Un auto recorre una trayectoria circular de 304.8m una velocidad de vt193.6 k/h
¿calcular su aceleración angular?
.r = 304.8m
.vt = 193.6k/h
ac = vt2/r ac = (536m/s2) / 304.8m = 9.426 m/s2
(193.6 km / 1h ) * (1h / 3600s ) * (100m / 1km )
Un volante aumenta su velocidad de rotacion de 6 a 12 rev x s ¿Cuál es su aceleración angular?
Wi = 6 rev / s 0.6280 (12) = 7.5360
Wi = 12 rev 0.6180 (6) = 3.7680
T = 2s
A = ? a = 7.5360 – 3.7680 / 2 = 18.84 r / s2
domingo, 11 de mayo de 2008
FRECUENCIA Y PERIODO
En el movimiento circular uniforme 1 vuelta = 1 circulo complete = 360˚ = 1 rev
La palabra frecuencia (f) indica el numero de revoluciones, vueltas, círculos completos.
Sus unidades corresponde a círculos/s también llamados Hertz 1 Hertz (Hz) corresponde a 1 vuelta en 1 s
1c/s = 1Hz
el periodo t indica el tiempo pues tarda una particula en realizar 1 circulo copleto.
La unidad utilizada en el periodo es el segundo.
El periodo t y la frecuencia f son cantidades reciprocas.
Por ejemplo si la frecuencia f es de 10c/s
El tiempo tarda en realizar un circulo completo es de 1/10s
F = 1/T ECUACION
T = 1/F ECUACION
T periodo en s
F periodo c/s
Los conceptos de frecuencia y periodo son muy utiles para comprender los fenómenos que se producen en lo movimientos, periodos, estos fenómenos se veran con mayor detenimiento de acustica, optica y electricidad.
Para incluir el concepto de periodo en las formulas de velocidad angular y velocidad tangencial, el periodo (t) sustituyen al tiempo, como se puede observar en las siguientes formulas.
W = 2PI/T ECUACION
VT = 2PIR/T ECUACION
Considerando con la frecuencia f es el resifrico de (t) las formulas toman la siguiente formula.
W = 2PIF ECUACION
VT = 2PIRF ECUACION
La palabra frecuencia (f) indica el numero de revoluciones, vueltas, círculos completos.
Sus unidades corresponde a círculos/s también llamados Hertz 1 Hertz (Hz) corresponde a 1 vuelta en 1 s
1c/s = 1Hz
el periodo t indica el tiempo pues tarda una particula en realizar 1 circulo copleto.
La unidad utilizada en el periodo es el segundo.
El periodo t y la frecuencia f son cantidades reciprocas.
Por ejemplo si la frecuencia f es de 10c/s
El tiempo tarda en realizar un circulo completo es de 1/10s
F = 1/T ECUACION
T = 1/F ECUACION
T periodo en s
F periodo c/s
Los conceptos de frecuencia y periodo son muy utiles para comprender los fenómenos que se producen en lo movimientos, periodos, estos fenómenos se veran con mayor detenimiento de acustica, optica y electricidad.
Para incluir el concepto de periodo en las formulas de velocidad angular y velocidad tangencial, el periodo (t) sustituyen al tiempo, como se puede observar en las siguientes formulas.
W = 2PI/T ECUACION
VT = 2PIR/T ECUACION
Considerando con la frecuencia f es el resifrico de (t) las formulas toman la siguiente formula.
W = 2PIF ECUACION
VT = 2PIRF ECUACION
VELOCIDAD ANGULAR
Como en el movimiento rectilíneo uniforme la velocidad angular es el resultado de dividir el desplazamiento angular entre el tiempo trascurrido de esta manera, las formulas anteriores de desplazamiento se aplican a las ecuaciones de velocidad angular.
Deacuerdo con la velocidad promedio entre dos puntos se tiene: Velocidad media = d/t. si el desplazamiento angular t para n vueltas 2πn rad/s, la formula para la velocidad angular es W = 2πn/t
W = Velocidad angular ( rad/s)
Π = 3.1416
N = Numero de revoluciones (n de vueltas)
T = Tiempo (s)
Para calcular la velocidad tangencial (1/t) en cm/s o en m/s considera el r.
Vt = 2πrn/t
Donde:
Vt = velocidad tangencial m/s o cm/s
Π = 3.1416
R = Radios de la circunferencia
N = Numero de revoluciones (n de vueltas)
T = Tiempo (s)
Ejemplo:
Calcula la velocidad angular en rad/s por la Vt cm/s de un disco de 20 cm de radio que jira a 33r.p.m aunque la velocidad angular se puede expresar en revoluciones x minuto (rpm) en la mayor parte de los problemas físicos usar rad por s (rad/s) para adaptarse a formulas convencionales.
Datos
R = 20cm
W = 33rpm
Π = 3.1416
Velocidad angular W = rad/s
Velocidad tangencial vt = cm/s
Ecuación 29 vt = Wr
33rev/min (1min/60s) (6.28/1rev) = 3.4540
min
rev – rad 3.45 * 20 = 69
Deacuerdo con la velocidad promedio entre dos puntos se tiene: Velocidad media = d/t. si el desplazamiento angular t para n vueltas 2πn rad/s, la formula para la velocidad angular es W = 2πn/t
W = Velocidad angular ( rad/s)
Π = 3.1416
N = Numero de revoluciones (n de vueltas)
T = Tiempo (s)
Para calcular la velocidad tangencial (1/t) en cm/s o en m/s considera el r.
Vt = 2πrn/t
Donde:
Vt = velocidad tangencial m/s o cm/s
Π = 3.1416
R = Radios de la circunferencia
N = Numero de revoluciones (n de vueltas)
T = Tiempo (s)
Ejemplo:
Calcula la velocidad angular en rad/s por la Vt cm/s de un disco de 20 cm de radio que jira a 33r.p.m aunque la velocidad angular se puede expresar en revoluciones x minuto (rpm) en la mayor parte de los problemas físicos usar rad por s (rad/s) para adaptarse a formulas convencionales.
Datos
R = 20cm
W = 33rpm
Π = 3.1416
Velocidad angular W = rad/s
Velocidad tangencial vt = cm/s
Ecuación 29 vt = Wr
33rev/min (1min/60s) (6.28/1rev) = 3.4540
min
rev – rad 3.45 * 20 = 69
DES PLEZAMIENTO ANGULAR
El desplazamiento angular es la velocidad recorrida por un cuerpo que sigue una trayectoria circulr y se expresa frecuente mente en (rad) (g) (c) (rev); estas unidades, el radian es el mas utilizado.
Puesto que la circunferencia entera de un circulo es presisa mente 2π veses en un sirculo completo ay 2 rad.
1rev = 2π rad = 360˚
pueato que π = 3.1416 
Puesto que la circunferencia entera de un circulo es presisa mente 2π veses en un sirculo completo ay 2 rad.
1rev = 2π rad = 360˚
pueato que π = 3.1416
1rad = 360˚/2π = 57.3˚
Ejemplo 1:
A cuantos rad/s corresponde 360˚ * min
360˚/1 = rev/min (6.28rad/1rev) (1min/60s)
rev/min = rad/seg = 2.260.8rad/60s = 37.68rad/s
Eemplo 2:
Cuantos g * s se desplaza 1 punto que gira 1400rev * 1
(1400/60s) (360/1) = 8.400˚/s
Ejemplo 3:
A cuantos rad/s corresponde 360˚ * min
360˚/1 = rev/min (6.28rad/1rev) (1min/60s)
rev/min = rad/seg = 2.260.8rad/60s = 37.68rad/s
Eemplo 2:
Cuantos g * s se desplaza 1 punto que gira 1400rev * 1
(1400/60s) (360/1) = 8.400˚/s
Ejemplo 3:
Un punto que ha girado 3.500˚ en 1 min ¿a cuantos rev * min corresponde?
(3.500˚/min) (1rev/360˚) = 9.72rev
Ejemplo 4:
A cuantos g * min corresponde 240 rev/s
240rev/s (360˚/1rev) (60s/1min) = 5.184 * 1060/m = 5184000.0
Ejemplo 5:
(3.500˚/min) (1rev/360˚) = 9.72rev
Ejemplo 4:
A cuantos g * min corresponde 240 rev/s
240rev/s (360˚/1rev) (60s/1min) = 5.184 * 1060/m = 5184000.0
Ejemplo 5:
un disco con diametro (0) de 20cm. Tiene en su borde una moneda después de 12rev rad 10cm.
¿Cuántos centímetros se habra desplazado?
¿Cuántos radianes se habra desplazado?
Si 2π r= 1rev = 2(3.1416)(10) =(62.83)(12rev)
=753.98cm
Ejemplo 6:
Un punto en el vorde de un disco de 80m de radio se desplaza en un angulo de 37˚ calcula lo siguiente:
¿Cuántos rad se desplazan?
¿Cuántas rev se desplazan?
¿Cuál es la longitud del arco descrito por el punto?
1rad = 57.3
37˚ (1rad/57.3) = 0.6457rad
0.6457rad (1rev/6.28) = 0.1028rev
0.1028rev/1 = 2π/1rev
0.1028rev/1 = 2(3.1416) (80) /1rev =0.1028rev/1
= 502.65cm/1rev = 51.67 cm
¿Cuántos centímetros se habra desplazado?
¿Cuántos radianes se habra desplazado?
Si 2π r= 1rev = 2(3.1416)(10) =(62.83)(12rev)
=753.98cm
Ejemplo 6:
Un punto en el vorde de un disco de 80m de radio se desplaza en un angulo de 37˚ calcula lo siguiente:
¿Cuántos rad se desplazan?
¿Cuántas rev se desplazan?
¿Cuál es la longitud del arco descrito por el punto?
1rad = 57.3
37˚ (1rad/57.3) = 0.6457rad
0.6457rad (1rev/6.28) = 0.1028rev
0.1028rev/1 = 2π/1rev
0.1028rev/1 = 2(3.1416) (80) /1rev =0.1028rev/1
= 502.65cm/1rev = 51.67 cm
VELOCIDAD INSTANTANEA
Para analizar el movimiento de una partícula se requiere conocer el valor de la velocidad en tramos pequeños de su trayectoria para ello se utiliza el concepto velocidad instantánea si pretendemos hacer imperceptibles los tramos de una trayectoria debemos aumentar el numero de intervalos asiéndolos mas diminutos en el limite.
¿Qué es un tramo mas pequeño de lo que podemos imaginar pero distinto de cero?
Necesitamos conocer la velocidad asociada a cada uno de los puntos de la trayectoria.
Para realizar este proceso debemos calcular la velocidad media entre dos puntos lo mas cercanos posible. Así, la velocidad instantánea de una partícula en el movimiento (t) es el limite de su velocidad media la de un intervalo de tiempo que incluya a t cuando el tamaño del intervalo tiende a cero.
Velocidad instantanea = lim= Ad
At At = 0
¿Qué es un tramo mas pequeño de lo que podemos imaginar pero distinto de cero?
Necesitamos conocer la velocidad asociada a cada uno de los puntos de la trayectoria.
Para realizar este proceso debemos calcular la velocidad media entre dos puntos lo mas cercanos posible. Así, la velocidad instantánea de una partícula en el movimiento (t) es el limite de su velocidad media la de un intervalo de tiempo que incluya a t cuando el tamaño del intervalo tiende a cero.
Velocidad instantanea = lim= Ad
At At = 0
La aceleración se define como la razón de cambio de con el intervalo de tiempo en el cual ocurre.
La aceleración es una magnitud pectorial es decir tiene magnitud y dirección para comprender este tema nos restringiremos ala aceleración de magnitud constante como lo hace la aceleración gravitacional.
Vinst = d2 - d1 / t2 - t1
.d2 = 30 m Vinst = 30 m – 5 m / 6 s – 2 s = 25 m / 4 s = 6.25 m / s
.d1 = 5 m
.t2 = 6 s
.t1 = 2 s
La aceleración es una magnitud pectorial es decir tiene magnitud y dirección para comprender este tema nos restringiremos ala aceleración de magnitud constante como lo hace la aceleración gravitacional.
Vinst = d2 - d1 / t2 - t1
.d2 = 30 m Vinst = 30 m – 5 m / 6 s – 2 s = 25 m / 4 s = 6.25 m / s
.d1 = 5 m
.t2 = 6 s
.t1 = 2 s
EJEMPLO:
Datos
a = a = vf – vi / tf – ti
vi = 2 m / s
vf = 8 m / s a = 8 m / s – 2 m / s / 4 s – 2 s
ti = 2 s = 6 m / s / 2 s = 3 m / s2
tf. =4 s
En un intervalo de 2˚a 4˚ la velocidad de un automóvil aumenta. Calcular grafica mente y matemáticamente de la aceleración.
Datos
a = a = vf – vi / tf – ti
vi = 2 m / s
vf = 8 m / s a = 8 m / s – 2 m / s / 4 s – 2 s
ti = 2 s = 6 m / s / 2 s = 3 m / s2
tf. =4 s
En un intervalo de 2˚a 4˚ la velocidad de un automóvil aumenta. Calcular grafica mente y matemáticamente de la aceleración.
Ejemplo 2:
Una camioneta lleva una velocidad inicial de 6 m/s al cabo de 4 s incrementa su velocidad a 20 m/s
¿Cuál es su aceleración y que distancia recorre?
.a = 3.5 d = vi + vf / 2
vi = d = 6 m / s + 20 m / s / 2 (c/s)
vf = d = 26 m / s /2 (c/s)
tf = d = (13 m/s) (c/s)
ti = d = 52 m
Ejemplo 4:
Un automóvil con velocidad inicial de 5 m/s acelera durante 12 s a 3 m/s2 ¿Cuál es la velocidad final?
¿Qué distancia recorre durante ese tiempo?
.a = 3 m/s2 vf = vi + at
vi = 5 m/s2 vf = 5 m/s2 + (3 m/s2) (12s)
vf = vf = 5 m/s2 + 36
t = 12s vf = 41 m/s
d = vi – vf / 2 *t
d = 5 m/s + 41 m/s (12)
d = 46/2 (12)
d = 23 (12)
d = 276 m
Ejemplo 6:
Un tren viaja a 8 m/s2 cuando de golpe se abre completamente la válvula de paso, lo que implica un cambio uniforme de velocidad, y se mantiene abierta durante una distancia de 1.5 k. si la aceleración de 0.20 m/s2 y es constantemente. ¿Cuál es la velocidad final?
.a = 0.20 m/s2
vi = 8 m/s2 vf2 = vi2 + 2 ad
d = 1500 M
Ejemplo:
Datos
.vi = 8 m/s vf2 = vi2 + 2 ad
a = 0.2 m/s2 = (8m/s)2 + 2 (0.2m/s2) (1500)
d = 1.5 km 1500 m = 64m2/s2 + 600m2/s2
vf = = 664m2/s2
= vf = r2 (664m/s)= 25.76m/s
Definición del movimiento circular uniforme mcu la rueda de la fortuna en movimiento circular uniforme una silla de la misma rueda realaza una trayectoria circular. Y sucede que puede tener una rapidez constante. Sin embargo como la velocidad es un vector, la rueda cambia a cada instante pues se dirige siempre de manera tangencial y forma un Angulo de 90˚ con el radio de giro.
En un momento dado, una persona que este sentada sin cinturón de seguridad puede salir disparada y en línea recta debido a que su movilidad es perpendicular al radio de giro.
TRALLECTORIA DISTANCIA Y DESPLAZAMIENTO
EL MOVIMINTO RECTILINEO UNIFORME
TRAYECTORIA
Es la línea que une las diferentes posiciones que ocupa un punto que se mueve en el espacio a medida que pasa el tiempo.
DISTANCIA
Es una magnitud escalar pues es únicamente la separación que existe entre dos puntos se puede expresar en m,s,km o en cualquier otra unidad equivalente.
VELOSIDAD Y RAPIDEZ
La velocidad se puede definir como el desplazamiento que efectúa una partícula entre el tiempo que tarda en realizarlo.
V= m/s
V= km/h
1) para ir al puerto de progreso en Yucatán, que esta a una distancia de 30 km al norte de la ciudad de Mérida, un automovilista viaja por una carretera recta a distintas velocidades 60 km/h durante 0.1 h 30 km/h durante 0.2 h. hasta su llegada.
¿Cuál será la distancia que recorran para cada tiempo especificado; su velocidad promedio y su velocidad media?
V= d/t
d= (v) (t)
t1= 0.1 h d1= v1*t1= (60 km/h)*(0.1 h)= 6 km
t2= 0.2 h d2= v2*t2= (30 km/h)*(0.2 h)= 6 km
t3= 0.3 h d3= v3*t3= (60 km/h)*(0.3 h)= 18 km
30 km
v= v1+v2+v3 = 60+30+60 km/h= 150 km/h
3 3 3
cuando d2= 30 km, d2= 12 km, t2=0.6 h, t1=0.1 h
30 km-12 km= 18 km= 60 km/h
0.6 h -0.3 h 0.3 h
cuando d2= 30 km, d1= 6 km, t2= 0.6 h, t1= 0.1 h
30 km-6 km= 24 km= 48 km/h
0.6 – 0.1 h 0.5 h
formula para el calculo del desplazamiento con la velocidad media.
d= vi + vf t
2
para un tiempo de 2 a 5 segundos la velocidad varia de 4 a 10 m/s cual será el desplazamiento.
t 1=25
tf = 55 d= 4m/s+10m/s=14m=7m/s
vi= 4 m/s 2 2
vf = 10 m/s d= 4m/s-10m/s=6m/2
d= 2 2
para realizar un viaje desde la ciudad de México desde un punto de la republica se utilizan 7 horas para recorrer una distancia de 700 km al origen 01 y al destino d2.
¿Cuál es su velocidad media?
0km+700= 100 km/h
0 h + 7 h
una mujer recorre una trayectoria rectilínea en su camioneta. Primero a una velocidad constante de 50 km/h y después a una velocidad de 70 km/h y al final a una de 60 km/h.
¿Cuál será la velocidad promedio?
DATOS
V1= 50 km/h v promedio = 50+70+60= 60 km/h
V2= 70 km/h 3
V3= 60 km/h
Velocidad promedio v1+vz+vn
n
Velocidad media d2-d
t2-t1
TRAYECTORIA
Es la línea que une las diferentes posiciones que ocupa un punto que se mueve en el espacio a medida que pasa el tiempo.
DISTANCIA
Es una magnitud escalar pues es únicamente la separación que existe entre dos puntos se puede expresar en m,s,km o en cualquier otra unidad equivalente.
VELOSIDAD Y RAPIDEZ
La velocidad se puede definir como el desplazamiento que efectúa una partícula entre el tiempo que tarda en realizarlo.
V= m/s
V= km/h
1) para ir al puerto de progreso en Yucatán, que esta a una distancia de 30 km al norte de la ciudad de Mérida, un automovilista viaja por una carretera recta a distintas velocidades 60 km/h durante 0.1 h 30 km/h durante 0.2 h. hasta su llegada.
¿Cuál será la distancia que recorran para cada tiempo especificado; su velocidad promedio y su velocidad media?
V= d/t
d= (v) (t)
t1= 0.1 h d1= v1*t1= (60 km/h)*(0.1 h)= 6 km
t2= 0.2 h d2= v2*t2= (30 km/h)*(0.2 h)= 6 km
t3= 0.3 h d3= v3*t3= (60 km/h)*(0.3 h)= 18 km
30 km
v= v1+v2+v3 = 60+30+60 km/h= 150 km/h
3 3 3
cuando d2= 30 km, d2= 12 km, t2=0.6 h, t1=0.1 h
30 km-12 km= 18 km= 60 km/h
0.6 h -0.3 h 0.3 h
cuando d2= 30 km, d1= 6 km, t2= 0.6 h, t1= 0.1 h
30 km-6 km= 24 km= 48 km/h
0.6 – 0.1 h 0.5 h
formula para el calculo del desplazamiento con la velocidad media.
d= vi + vf t
2
para un tiempo de 2 a 5 segundos la velocidad varia de 4 a 10 m/s cual será el desplazamiento.
t 1=25
tf = 55 d= 4m/s+10m/s=14m=7m/s
vi= 4 m/s 2 2
vf = 10 m/s d= 4m/s-10m/s=6m/2
d= 2 2
para realizar un viaje desde la ciudad de México desde un punto de la republica se utilizan 7 horas para recorrer una distancia de 700 km al origen 01 y al destino d2.
¿Cuál es su velocidad media?
0km+700= 100 km/h
0 h + 7 h
una mujer recorre una trayectoria rectilínea en su camioneta. Primero a una velocidad constante de 50 km/h y después a una velocidad de 70 km/h y al final a una de 60 km/h.
¿Cuál será la velocidad promedio?
DATOS
V1= 50 km/h v promedio = 50+70+60= 60 km/h
V2= 70 km/h 3
V3= 60 km/h
Velocidad promedio v1+vz+vn
n
Velocidad media d2-d
t2-t1
EL PESO
Como se dijo en el tema de aceleración de la gravedad, la tierra ejerce una atracción sobre todos los cuerpos y les imprime una aceleración promedio de 9.8 m/s2.
Como el peso de un cuerpo representa la fuerza con que la tierra atrae su masa, se tiene que si F= ma por la aceleración de la gravedad (A) toma el valor de la aceleración debido ala gravedad (B) por lo tanto se tiene:
p= peso del cuerpo en newtons o dinas.
m= masa del cuerpo en kg.
g= aceleración de la gravedad 9.8 m/s2 o 980 cm/s2.
El valor que tiene un kilogramo masa al ser atraído por la tierra, corresponde a la fuerza que acelera dicha masa en el centro del planeta.
T – 98.1 N = 10 Kg * a
-T – 147 15 N = 15 kg * a
49.05 N = 25 kg * a
a=49.05 kg m/s2 = 1.96 m/s2
25 kg
T- 98.1 N = 10 kg * 1.96 m/s2
T- 98.1 N = 10.6 kg m/s2
T= 19.6 kg m/s2198.1 kg m/s2
T= 117.7 kg m/s2
un elevador que tiene un peso de 800 N sube acelerando a 2 m/s.
¿Cuál será el valor de la tensión del cable que soporta dicho elevador?
p= 8000 N p= m* a m= 8000 kg m/s2
a= 2 m/s2 m= p/g 9.81 m/s2
g= 9.81 m/s2 m= 815.99 kg
T- 8000 N = p/g * 2 m/s2
T- 8000 N = 815.14 kg m/s2
T= 1630.9 kg m/s +8000 kg m/s2
T= 9630.98 kg m/s2
Como el peso de un cuerpo representa la fuerza con que la tierra atrae su masa, se tiene que si F= ma por la aceleración de la gravedad (A) toma el valor de la aceleración debido ala gravedad (B) por lo tanto se tiene:
p= peso del cuerpo en newtons o dinas.
m= masa del cuerpo en kg.
g= aceleración de la gravedad 9.8 m/s2 o 980 cm/s2.
El valor que tiene un kilogramo masa al ser atraído por la tierra, corresponde a la fuerza que acelera dicha masa en el centro del planeta.
1) que aceleración en m/s2 y en cm/s2 imprimirá una fuerza de 20 newtons a un objeto de 10 kg de masa.
2) Calcular la masa de una persona cuyo peso es de 890 newtons.
3) Un cuerpo de 40 kg m esta suspendido del extremo de un cable. ¿Cuál será la tensión Ta del cable si se jala hacia arriba con una aceleración de 5 m/s2 y cual será la tensión Tb si se jala con una aceleración de 5 m/s2 hacia abajo?.
DATOS
m= 40 kg
a= 5 m/s2
peso = mg = (40 kg) (9.8 m/s2) =392 N
Ta= 592 N
Tb= 192 N
Como la aceleración se dirige hacia arriba la fuerza resultante es:
T- 392 = m*a
Para Ta se tiene:
Ta= 392 N + 40 kg *5m/s2
=392 N + 200 N
=592 N
Tb = 392 N – 40 kg *5m/s2
=392 N – 200N
=192 N
se tiene un disco del cual se suspenden dos masas = 10 kg y 15 kg. Calcular la tensión en la cuerda y la aceleración en cada lado.
P1= (10 kg) (9.81 m/s2) = 98.1 kg m/s2 N
P2= (15 kg) (9.81 m/s2) = 147.15 kg m/s2 N
A) para la masa de 10 kg (98.1 N) se aplica la fuerza resultante que debe ser igual a la masa por la aceleración Asia arriba.
T- 98.1 N = 10 kg * a
m= 40 kg
a= 5 m/s2
peso = mg = (40 kg) (9.8 m/s2) =392 N
Ta= 592 N
Tb= 192 N
Como la aceleración se dirige hacia arriba la fuerza resultante es:
T- 392 = m*a
Para Ta se tiene:
Ta= 392 N + 40 kg *5m/s2
=392 N + 200 N
=592 N
Tb = 392 N – 40 kg *5m/s2
=392 N – 200N
=192 N
se tiene un disco del cual se suspenden dos masas = 10 kg y 15 kg. Calcular la tensión en la cuerda y la aceleración en cada lado.
P1= (10 kg) (9.81 m/s2) = 98.1 kg m/s2 N
P2= (15 kg) (9.81 m/s2) = 147.15 kg m/s2 N
A) para la masa de 10 kg (98.1 N) se aplica la fuerza resultante que debe ser igual a la masa por la aceleración Asia arriba.
T- 98.1 N = 10 kg * a
B) para la masa de 15 kg (147.15 N) se aplica la fuerza resultante que debe ser igual a la masa por la aceleración hacia abajo.
147 N – T = 15 kg * a
147 N – T = 15 kg * a
T – 98.1 N = 10 Kg * a
-T – 147 15 N = 15 kg * a
49.05 N = 25 kg * a
a=49.05 kg m/s2 = 1.96 m/s2
25 kg
T- 98.1 N = 10 kg * 1.96 m/s2
T- 98.1 N = 10.6 kg m/s2
T= 19.6 kg m/s2198.1 kg m/s2
T= 117.7 kg m/s2
un elevador que tiene un peso de 800 N sube acelerando a 2 m/s.
¿Cuál será el valor de la tensión del cable que soporta dicho elevador?
p= 8000 N p= m* a m= 8000 kg m/s2
a= 2 m/s2 m= p/g 9.81 m/s2
g= 9.81 m/s2 m= 815.99 kg
T- 8000 N = p/g * 2 m/s2
T- 8000 N = 815.14 kg m/s2
T= 1630.9 kg m/s +8000 kg m/s2
T= 9630.98 kg m/s2
TIRO VERTICAL
El tiro vertical es un movimiento hacia arriba y en línea recta la velocidad disminuye conforme asciende.
La aceleración de la gravedad retarda el movimiento del cuerpo hasta que este se detiene y empieza a caer de vuelta a la superficie de la tierra, entonces aumenta su velocidad y alcanza la misma que tenia en el punto donde se lanzo. El tiempo empleado hasta llegar al punto mas alto es igual al tiempo que tarda en la caída. Por lo tanto los movimientos para cualquier punto a lo largo de la trayectoria están determinados por las ecuaciones para la caída libre.
La aceleración de la gravedad retarda el movimiento del cuerpo hasta que este se detiene y empieza a caer de vuelta a la superficie de la tierra, entonces aumenta su velocidad y alcanza la misma que tenia en el punto donde se lanzo. El tiempo empleado hasta llegar al punto mas alto es igual al tiempo que tarda en la caída. Por lo tanto los movimientos para cualquier punto a lo largo de la trayectoria están determinados por las ecuaciones para la caída libre.
Sin importar que el cuerpo se mueve hacia arriba o hacia abajo la aceleración debido a la gravedad tendrá dirección hacia abajo por convención los valore de 6 serán positivos cuando el cuerpo este en descenso y serán negativos cuando el cuerpo este en asenso.
1) una pelota de béisbol es lanzada hacia arriba con una velocidad de 20m/s. calcular:
A)la altura máxima a la que llega la pelota.
B)la velocidad al regresar al punto de partida.
C)el tiempo total requerido para volver al punto total de lanzamiento.
A)la altura máxima a la que llega la pelota.
B)la velocidad al regresar al punto de partida.
C)el tiempo total requerido para volver al punto total de lanzamiento.
viernes, 7 de marzo de 2008
CAIDA LIBRE
Los cuerpos en caida libre no son mas que un caso en particular del movimiento rectilineo uniformemente acelerado, con la caracteriztica de que la aceleracion se deve a la accion de la gravedad.
Un cuerpo tiene caida libre si desiende de manera perpendicular a la superfisie de la tirra asignada por el aire.
La aceleracion de la gravedad siempre esta dirigida hacia abajo (hacia el centro de la tierra) y se acostumbra representarla con la letra (g).Para fines practicos se le da un valor de g=9.8 m/s2 o g= 980 cm/s2 o g= 32 pies/s2.
Un cuerpo tiene caida libre si desiende de manera perpendicular a la superfisie de la tirra asignada por el aire.
La aceleracion de la gravedad siempre esta dirigida hacia abajo (hacia el centro de la tierra) y se acostumbra representarla con la letra (g).Para fines practicos se le da un valor de g=9.8 m/s2 o g= 980 cm/s2 o g= 32 pies/s2.
2 paredes están a una distancia de 6 metros. ( véase en la figura ); un objeto cuyo peso es de 1200N esta en el centro de una cuerda y forma ángulos de 40° y 30° calcula el valor de las tenciones de cada una de las cuerdas.
T1/sen(60)= T2/sen(50)=1200N/sen(70)
T1/0.866= T2/0.766= 1200/0.939
T1=(1200)(0.866)/0.939= 1106.7
T2=(90)(0.939)/0.939= 978.9
T1/0.866= T2/0.766= 1200/0.939
T1=(1200)(0.866)/0.939= 1106.7
T2=(90)(0.939)/0.939= 978.9
EJEMPLO 2
Una piñata que pesa 90N se suspende de dos postes, como se muestra en la siguiente figura calcula las tenciones de las 2 cuerdas
F1/ sen (85) = F2/ sen (80) = 90N/ sen (15)
F1/ 0.996 = F2/ 0.984 = 90N/ 0.258
F1 = (90N) * (0.258) / 0.258 = 343. 25N
F2 = (90N) * (0.284) / 0.258 = 343.25N
F1/ 0.996 = F2/ 0.984 = 90N/ 0.258
F1 = (90N) * (0.258) / 0.258 = 343. 25N
F2 = (90N) * (0.284) / 0.258 = 343.25N
EJEMPLO 1
Un semáforo esta suspendido de 2 soportes, las 3 fuerzas que actúan a partir de un punto en común se llama “o” Fg, el peso del semáforo es de 500n y que actúa en línea recta hacia abajo: F1 la tensión de un cable a 45 gr. hacia arriba y ala izquierda, y F2 la tensión de otro cable a 30 grados hacia arriba y a la derecha.
Calculemos grafica y analítica mente las magnitudes de las tenciones.
Calculo analítico los ángulos internos del triangulo se determinan con los ángulos externos complementarios después, se aplica la ley de los senos para encontrar las longitudes de los lados (a c) y (b c) utilizando los ángulos dados en la figura anterior. Y luego tenemos que
A = 45°
B = 60°
C = 75°
F1/ sen B = F2/ sen A = Fg/ sen C
F1/ sen (60) = F2/ sen (95) = 500n/ sen (75)
F1/ 0.866 = F2/ 0.707 = 500N/ 0.965
Calculemos grafica y analítica mente las magnitudes de las tenciones.
Fg = 500N
F1 =
F2 =
θ = 45°
θ = 30°
F1 =
F2 =
θ = 45°
θ = 30°
Calculo analítico los ángulos internos del triangulo se determinan con los ángulos externos complementarios después, se aplica la ley de los senos para encontrar las longitudes de los lados (a c) y (b c) utilizando los ángulos dados en la figura anterior. Y luego tenemos que
A = 45°
B = 60°
C = 75°
F1/ sen B = F2/ sen A = Fg/ sen C
F1/ sen (60) = F2/ sen (95) = 500n/ sen (75)
F1/ 0.866 = F2/ 0.707 = 500N/ 0.965
EJEMPLO 3
Sobre un bloque de 196N de peso, que esta sobre una superfisie plana, se aplica una fuerza de 98N que forma un angulo de inclinacion de 30 grados respecto a la horizontal.
Al cabo de 3s la velocidad del bloque es de 9m/s.
Calcular el coeficiente de friccion dinamico.
P= 196N
F= 98N
t= 3s
Vf= 9m/s
grados= 30
a= Vf-Vi/t= (9m/s)(o)/3s= 3m/s2
Fx= Fcos 30= (98N)(0.866)= 84.86N
Fy= Fsen 30= (98N)(0.5)= 49N
F= Md-N= Md(P+Fsen30)
Md= (196N+49N)
Md= (245)
Fx-f= ma
84.86N-Md(245)= 196/9.8m/s2(3m/s2)
84.86N-Md(245)= 60n
Md= 60N+84.86N/245
Md=24.86N/245N
Md= 0.101
Al cabo de 3s la velocidad del bloque es de 9m/s.
Calcular el coeficiente de friccion dinamico.
P= 196N
F= 98N
t= 3s
Vf= 9m/s
grados= 30
a= Vf-Vi/t= (9m/s)(o)/3s= 3m/s2
Fx= Fcos 30= (98N)(0.866)= 84.86N
Fy= Fsen 30= (98N)(0.5)= 49N
F= Md-N= Md(P+Fsen30)
Md= (196N+49N)
Md= (245)
Fx-f= ma
84.86N-Md(245)= 196/9.8m/s2(3m/s2)
84.86N-Md(245)= 60n
Md= 60N+84.86N/245
Md=24.86N/245N
Md= 0.101
cos= Cateto adyasente/hipotenusa= Fx/F
sen= Cateto opuesto/hipotenusa= Fy/f
sen= Cateto opuesto/hipotenusa= Fy/f
m=P/g m=196Nkgm/s2 /9.81m/s2= 20
a= Vf-Vi/t=9m/s-0/3s=3m/s
Fx=F * cos=(98)(0.866)=84.86N
Fy= F * sen=(98)(0.5)=49
EJEMPLO 2
A un bloque de hierro de 400N de peso que se encuentra en una superfisie de hormigon cuyo coeficiente de friccion dinamica es de 0.3, se le aplica una fuerza de 196N durante 3 segundos.¿Cual es la velocidad que adquiere alcabo de ese tiempo?
P= 490N
Md= 0.3F= 196N
t= 3 s
Vf= 2.94 m/s
a= 0.98 m/s2
m= P/g= 490kgm/s2/9.81m/s2= 50 kg
f= P
Mdf= (490 kgm/s2) (0.3) = 147 kgm/s2 o N
a= F-f/m
a= 196N-147N/50kg= 49N/50kg=0.98m/s2
Vf= Vi+a tVf= 0+0.98m/s2 *3s
Vf= 2.94m/s
P= 490N
Md= 0.3F= 196N
t= 3 s
Vf= 2.94 m/s
a= 0.98 m/s2
m= P/g= 490kgm/s2/9.81m/s2= 50 kg
f= P
Mdf= (490 kgm/s2) (0.3) = 147 kgm/s2 o N
a= F-f/m
a= 196N-147N/50kg= 49N/50kg=0.98m/s2
Vf= Vi+a tVf= 0+0.98m/s2 *3s
Vf= 2.94m/s
EJEMPLO 1
Un cubo de metal de 600 newtons de peso esta en reposo sobre el piso de cemento; la fuerza horizontal para que inicie el movimiento es de 200 newtons y la fuerza para mantenerlo en moviento a velocidad constante de 150 newtons.Calcular:a) El coeficiente de fricción estáticob) El coeficiente de fricción dinámico
P= 600N Me= Fe/N Fe= ME N
V1= 0
Fe= 200N Md= Fd/N Fd= Md N
Fd= 150
N= 600
Me= 200N/600N= 0.33
Md= 150N/600N= 0.25
P= m * g
P= 600N Me= Fe/N Fe= ME N
V1= 0
Fe= 200N Md= Fd/N Fd= Md N
Fd= 150
N= 600
Me= 200N/600N= 0.33
Md= 150N/600N= 0.25
P= m * g
FRICCION O ROSAMIENTO
Siempre que un cuerpo se deslisa sobre otro se presenta una fuerza que se opone a su desplasamiento a esa fuerza selellama friccion.
jueves, 6 de marzo de 2008
jueves, 28 de febrero de 2008
MAGNITUD
LA MAGNITUD: Es todo lo que puede ser medido
UNIDADES FUNDAMENTALES
UNIDAD SIMBOLO MAGNITUD
Metro m Longitud
Kilogreamo Kg Masa
Segundo S Tiempo
Amperio A Intencidad de la corriente
Kelvin K Temperatura
Candela cd Intencidad luminosa
Mol mol Cantidad de materia
Newton N Fuerza
Joule J Energia
miércoles, 27 de febrero de 2008
METODO CIENTIFICO
1.- RECONOCER la existencia de un problema
2.- SUPONER una respuesta al problema
3.- PREDECIR las consecuencias de esa suposicion
4.- EFECTUAR los experimentos necesarios
5.- FORMULAS una teoria sencilla para comprobar el fenomeno
LA FISICA CLACICA : Estidia los fenomenos en los cuales las velocidades son muy pequeñas si se comparan con la velocidad de la luz.
LA FISICA MODERNA: Se encarga de los fenomenos relacionados con valores sercanos a ella.
2.- SUPONER una respuesta al problema
3.- PREDECIR las consecuencias de esa suposicion
4.- EFECTUAR los experimentos necesarios
5.- FORMULAS una teoria sencilla para comprobar el fenomeno
LA FISICA CLACICA : Estidia los fenomenos en los cuales las velocidades son muy pequeñas si se comparan con la velocidad de la luz.
LA FISICA MODERNA: Se encarga de los fenomenos relacionados con valores sercanos a ella.
jueves, 21 de febrero de 2008
CONOCIMIENTO CIENTIFICO
Es un pensamiento dinamico en la conciensia de las personas capaz de utilizar la reflixion critica sobre un problema.
El conocimiento cientifico va mas alla del conocimiento empirico por lo cual se aproxima mucho mas a la vedad, yaque busca las leyes y las causas que lo orginan. se adquiere atraves de pasos metodicos y reflexibos que nos ayudan a saber el que y porque de los fenomenos o hechos.
El conocimiento cientifico va mas alla del conocimiento empirico por lo cual se aproxima mucho mas a la vedad, yaque busca las leyes y las causas que lo orginan. se adquiere atraves de pasos metodicos y reflexibos que nos ayudan a saber el que y porque de los fenomenos o hechos.
FENOMENOS FISICOS
Los fenomenos fisicos estan vinculados o relasionados directa mente con la evolucion de la tecnologia y el desarrollo de la sociedad a lo largo de la istoria del hombre la fisica es una de las ciencias naturales que ha contribuido en gran medida al desarrollo al vien estar de la umanidad. gracias a su estudio e investigacion ha sido posible encontrar una ex plicacion cientifica a los fenomenos que se presentan a nuestra vida diaria.
SISTEMA FISICO.- es un agregado de odjetos o entidades materiales entre cuyas partes existe una vinculacion o interaccion de tipo casual. todos los sistemas fisicos se caracterisan por:
1.- tener una uvicacion en el especio-tiempo
2.- tener un estado fisico definido sujeto a evolucion temporal
3.- se puede asociar a una magnitud fisica llamada energia.
Los sistemas fisicos pueden ser abiertos o cerrados, segun se realize o no intercabios de energia con su entorno.
Un sistema abierto es un sistema que resibe flujos de energia y materia en su entorno.
Un sistema cerrado es entropico, es decir solo intercamvia energia dentro de si mismo.
Un sistema aislado no tiene ningun intercambio con el entorno.
SISTEMA FISICO.- es un agregado de odjetos o entidades materiales entre cuyas partes existe una vinculacion o interaccion de tipo casual. todos los sistemas fisicos se caracterisan por:
1.- tener una uvicacion en el especio-tiempo
2.- tener un estado fisico definido sujeto a evolucion temporal
3.- se puede asociar a una magnitud fisica llamada energia.
Los sistemas fisicos pueden ser abiertos o cerrados, segun se realize o no intercabios de energia con su entorno.
Un sistema abierto es un sistema que resibe flujos de energia y materia en su entorno.
Un sistema cerrado es entropico, es decir solo intercamvia energia dentro de si mismo.
Un sistema aislado no tiene ningun intercambio con el entorno.
UBICACION DE LA FISICA "2"
Para poder medir debemos estudiar 2 fenomenos o conseptos basicos
A) Cantidades Escalares
B) Cantidades Bectoriales
Las cantidades escalares son a quellas que tienen magnitud solamente. por ejemplo 30 manzanas, 8 kilogramos, 9 kilometros o 7 alumnos, etc.
Las cantidades bectoriales son aquellas que tienen magnitud y direccion. por ejemplo cundo el viento sopla a 40 km/hr en direccion sureste; la fuersa de 85 kgm aplicada al empujar un automovil o la velocidad de un avion que va de mexico a san luis potosi a 275 km/hr
A) Cantidades Escalares
B) Cantidades Bectoriales
Las cantidades escalares son a quellas que tienen magnitud solamente. por ejemplo 30 manzanas, 8 kilogramos, 9 kilometros o 7 alumnos, etc.
Las cantidades bectoriales son aquellas que tienen magnitud y direccion. por ejemplo cundo el viento sopla a 40 km/hr en direccion sureste; la fuersa de 85 kgm aplicada al empujar un automovil o la velocidad de un avion que va de mexico a san luis potosi a 275 km/hr
miércoles, 20 de febrero de 2008
martes, 19 de febrero de 2008
UNIDAD 2.- Mecanica
-Fuerza
-Fricciòn
-Equilibrio
-Fuerza gravitacional
-Impulso
-Masa
-Inersia
-Peso
-Aseleracion
-Cantidad de Movimiento
-Tipos de Movimiento
-Movimiento rectilineo uniforme
-Movimiento rectilineo uniforme mente acelerado
-Movimiento circular uniforme
-Movimiento circular uniforme acelerado
-Movimiento circular
-Movimiento armonico simple
-Energia mecanica
-Energia cientifica
-Energia potencial
-Interconvencion
-Trabajo mecanico
-Potencia
-Fricciòn
-Equilibrio
-Fuerza gravitacional
-Impulso
-Masa
-Inersia
-Peso
-Aseleracion
-Cantidad de Movimiento
-Tipos de Movimiento
-Movimiento rectilineo uniforme
-Movimiento rectilineo uniforme mente acelerado
-Movimiento circular uniforme
-Movimiento circular uniforme acelerado
-Movimiento circular
-Movimiento armonico simple
-Energia mecanica
-Energia cientifica
-Energia potencial
-Interconvencion
-Trabajo mecanico
-Potencia
UNIDAD 1.- conseptos introductorios
-Ubicacion de la signatura
-Relacion interdisiplinaria
-Fenomenos naturales
-Tecnologia y sociedad
-Sistemas fisicos
-Metodologia cientifico
-Conocimientos cientificos
-Relacion interdisiplinaria
-Fenomenos naturales
-Tecnologia y sociedad
-Sistemas fisicos
-Metodologia cientifico
-Conocimientos cientificos
miércoles, 13 de febrero de 2008
MATCH
Mach crítico
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
Se denomina Mach crítico al número de Mach de vuelo de una aeronave en el que el punto de máxima velocidad local del fluido (aire) que le rodea alcanza la velocidad del sonido. Esto último
equivale a que en dicho punto (el punto de máxima velocidad local del aire) se alcanza un Mach igual a 1. Cabe destacar que la velocidad del aire a la que nos referimos es la velocidad del aire respecto de la aeronave, no respecto de tierra.
El número de Mach crítico de cualquier aeronave es siempre inferior a 1, ya que en el campo fluido que rodea a la misma siempre hay puntos en los que la velocidad local es mayor que la velocidad de vuelo.
Cuando en una aeronave propulsada por hélices (aviones, helicópteros, convertiplanos), en algún punto de una hélice se da M=1, se crean una serie de turbulencias que hacen descender enormemente su rendimiento y que incluso pueden provocar la entrada en pérdida de la aeronave. Por lo tanto, el Mach crítico de una de estas aeronaves nos da una idea de la velocidad máxima que puede alcanzar sin que aparezcan las mencionadas turbulencias.
El número de Mach crítico es el punto de partida del régimen transónico. Debido al aumento considerable de la resistencia aerodinámica que los perfiles sufren cuando vuelan en torno a la velocidad del sonido, el Mach crítico es una primera aproximación a la velocidad máxima de vuelo de cualquier aeronave que haya sido diseñada para volar por debajo de la velocidad del sonido.
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
Se denomina Mach crítico al número de Mach de vuelo de una aeronave en el que el punto de máxima velocidad local del fluido (aire) que le rodea alcanza la velocidad del sonido. Esto último
equivale a que en dicho punto (el punto de máxima velocidad local del aire) se alcanza un Mach igual a 1. Cabe destacar que la velocidad del aire a la que nos referimos es la velocidad del aire respecto de la aeronave, no respecto de tierra.El número de Mach crítico de cualquier aeronave es siempre inferior a 1, ya que en el campo fluido que rodea a la misma siempre hay puntos en los que la velocidad local es mayor que la velocidad de vuelo.
Cuando en una aeronave propulsada por hélices (aviones, helicópteros, convertiplanos), en algún punto de una hélice se da M=1, se crean una serie de turbulencias que hacen descender enormemente su rendimiento y que incluso pueden provocar la entrada en pérdida de la aeronave. Por lo tanto, el Mach crítico de una de estas aeronaves nos da una idea de la velocidad máxima que puede alcanzar sin que aparezcan las mencionadas turbulencias.El número de Mach crítico es el punto de partida del régimen transónico. Debido al aumento considerable de la resistencia aerodinámica que los perfiles sufren cuando vuelan en torno a la velocidad del sonido, el Mach crítico es una primera aproximación a la velocidad máxima de vuelo de cualquier aeronave que haya sido diseñada para volar por debajo de la velocidad del sonido.
MECATRONICA
Yo soy Israel Cruz Ramos, estoy estudiando la carrera de mecatronica, me intereso por que 
enseñan a crear sensores y otros tipos de cosas, si pongo empeño por aprender todo lo vasico de la electronica pienso que en tendiendo eso sera mas fasil poder crear algo pequeño y sencillo asi con el tiempo y practica poder crear algo mas grandre, me gustaria aprender mas sobre carros es lo que mas me gusta e ido a ver exposiciones de mecatronica todo estava relacionado con carros , uvo uno que estuvo muy interesante, fue el de un carro que tenia un celular 
adaptado ala computadora eso creo, bueno lo que hicieron con el carro fue adaptarle el celular, tambien tenia una manguera que era la que proporciona la gasolina entonces lo que hacia el celular era avisar al dueño cuando estuvieran robando el carro, el dueño del carro esta abisado lo unico que aria seria poner una clave de su celular y el celular del carro se encarga de bloquear el paso de la gasolina los unicos que lo pueden arreglar son los que inventaron ese tipo de seguridad, bueno esto fue lo que entendi, a mi me gustaria al gun dia poder crear algo que se le pueda poner a un carro, bueno creo que por eso estoy estudiando mecatronica, espero que este bien redactado y lo pueda entender profe.
enseñan a crear sensores y otros tipos de cosas, si pongo empeño por aprender todo lo vasico de la electronica pienso que en tendiendo eso sera mas fasil poder crear algo pequeño y sencillo asi con el tiempo y practica poder crear algo mas grandre, me gustaria aprender mas sobre carros es lo que mas me gusta e ido a ver exposiciones de mecatronica todo estava relacionado con carros , uvo uno que estuvo muy interesante, fue el de un carro que tenia un celular 
adaptado ala computadora eso creo, bueno lo que hicieron con el carro fue adaptarle el celular, tambien tenia una manguera que era la que proporciona la gasolina entonces lo que hacia el celular era avisar al dueño cuando estuvieran robando el carro, el dueño del carro esta abisado lo unico que aria seria poner una clave de su celular y el celular del carro se encarga de bloquear el paso de la gasolina los unicos que lo pueden arreglar son los que inventaron ese tipo de seguridad, bueno esto fue lo que entendi, a mi me gustaria al gun dia poder crear algo que se le pueda poner a un carro, bueno creo que por eso estoy estudiando mecatronica, espero que este bien redactado y lo pueda entender profe.
Suscribirse a:
Entradas (Atom)